Research interests

The main research interest of my team is the theory of quantum many-body non-equilibrium physics. We're interested in advancing our fundamental understanding of complex quantum dynamics in large many-body models, by utilizing state-of-the-art numerical methods and quantum optics tools [e.g.: matrix product states (MPS)/tensor networks, discrete truncated Wigner approximations (DTWA), quantum trajectories, adiabatic elimination, ...]. Our research not only seeks new insight into fundmantal large-scale quantum theory (e.g. entanglement dynamics), but also finds applications in various experimental setups in condensed matter, cold atoms, quantum computers, and sometimes even chemistry.

Numerical methods for fundamental quantum many-body theory

[see e.g. Phys. Rev. X 5, 011022 (2015)]

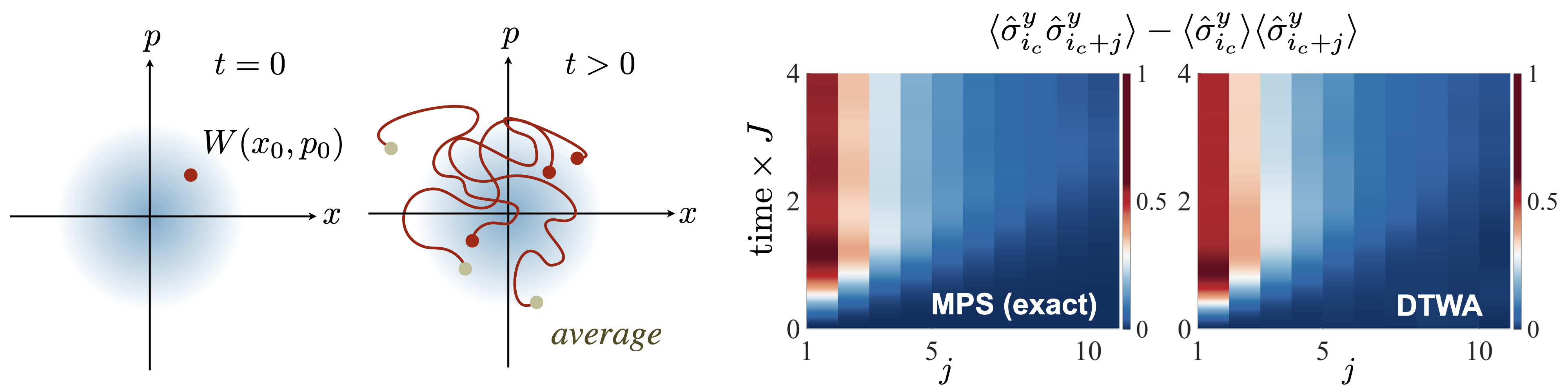
We are interested in developing new types of numerical methods for simulating and understanding quantum many-body dynamics on classical computers. In quantum mechanics, the Hilbert space grows exponentially with the number of particles. Remarkably, it is still not necessarily just the size of the system that makes a quantum evolution hard to simulate on a classical computer. Rather it is the amount of quantum entanglement in an evolution that can be linked to the question of "classical simulability". We are experts in so-called matrix product state (MPS)/tensor network techniques, which is a numerical approach for simulating quantum many-body evolution on truncated Hilbert spaces with restricted entanglement. A main recent research focus lies e.g. on finding a better understanding on how noise limits large-scale entanglement. In addition we are experts in new types of semi-classical phase space approaches, e.g. we developed a so-called discrete truncated Wigner approximation. It is based on the well-known truncated Wigner approximation (TWA), but adapted to discrete many-body models, utilizing a novel type of sampling of quantum noise from discrete (Wigner) distributions.

Dynamics and disorder in cavity-coupled molecules

[see e.g. Commun Phys 5, 120 (2022)]

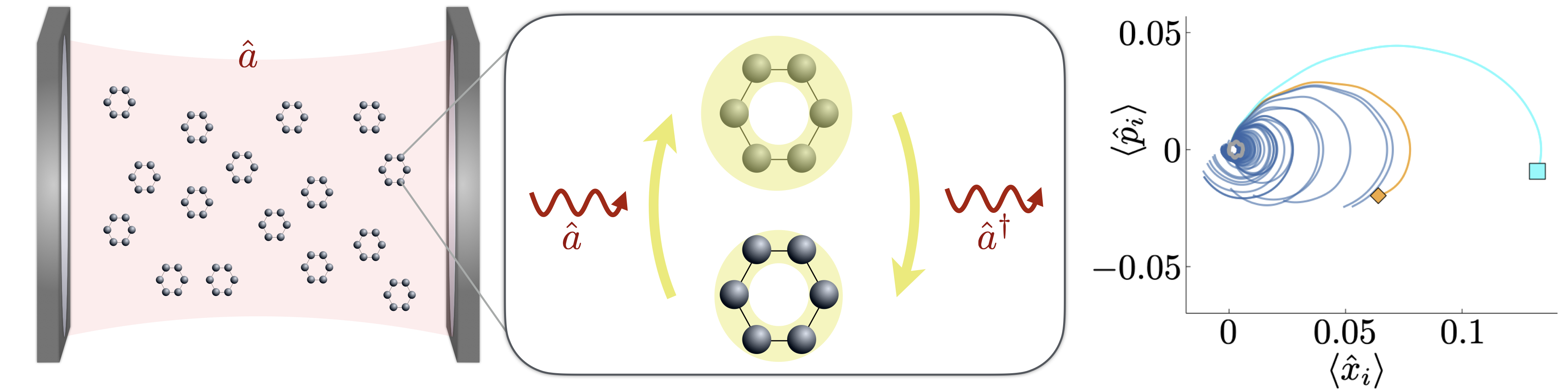
A cavity is (typcially) an arrangement of mirrors that fix the boundary condition for a particular mode of the electromagnetic field (e.g. for an optical or a microwave photon). If a resonant emitter inside a cavity emitts a photon, it remains trapped around the emitter. For sufficiently good cavities the emitter and the cavity-mode then exchange energy more quickly than they can both dissipate it. Such a scenario is denoted as strong coupling, and in strong coupling regimes the emitters and the cavity-mode have to be considered as one single entity with new hybridized modes. Experiments in Strasbourg (Laboratoire des nanostructures, T. W. Ebbesen) have pioneered the idea of strongly and collectively coupling transitions in molecular ensembles to cavities (or other types of resonant modes), and shown that this can lead to a modification of chemical reactivity or other material properties. We are interested in exploring many-body dynamics in minimal quantum optics models for systems of cavity-coupled many-body systems, to shed light on physical mechanisms behind such experimental observations.

Applications in cold atoms

[see e.g. Nature Communications 10, 1714 (2019)]

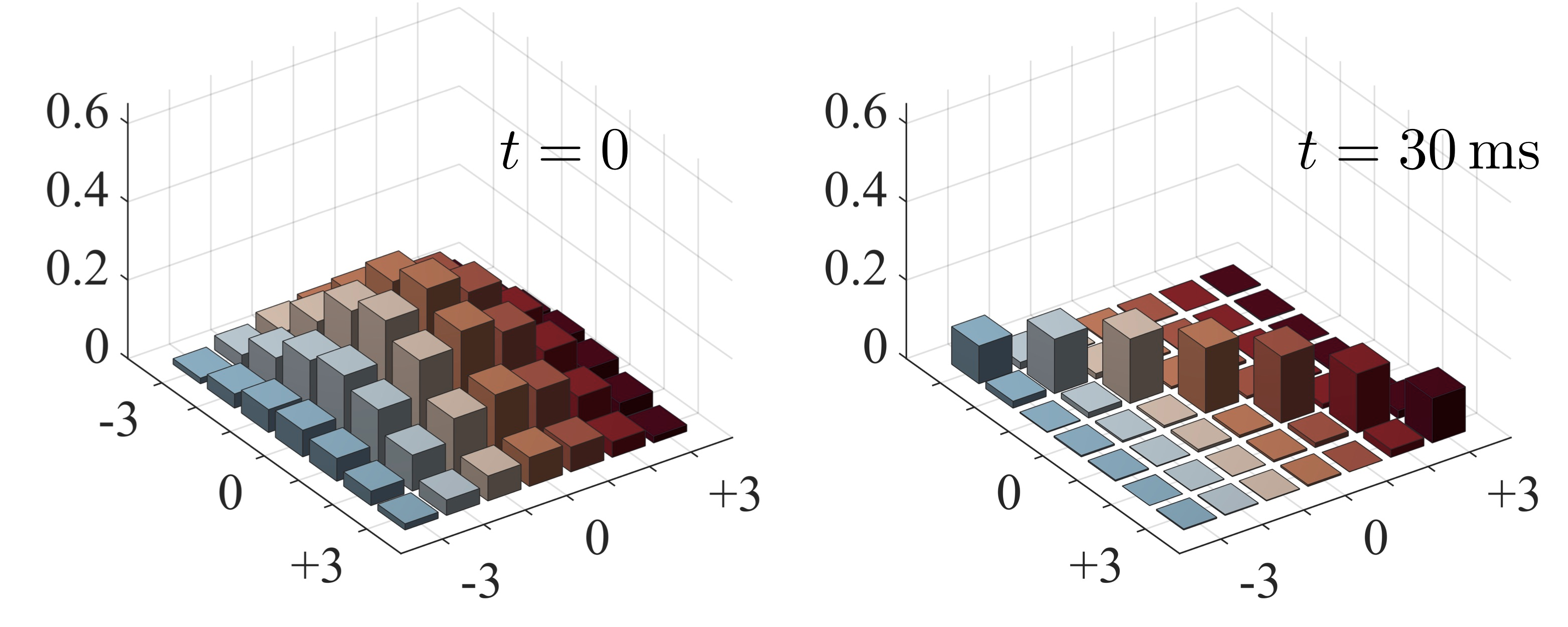
Over the past years, technological progress has made it possible to cool atoms (with lasers) to extremely low temperatures, and to trap them in controllable optical potentials (in so-called "optical lattices" or "optical tweezers"), e.g. in experiments in Strasborg (Exotic quantum matter laboratory, S. Whitlock). We are interested in theoretically modeling dynamics of such systems of "interacting atoms trapped in crystals of light''. Being well isolated from any type of environment, such setups allow a controlled experimental observation of (almost) coherent quantum many-body evolution with interactions. We are interested in utilizing such new setups for studying fundamental effects in quantum many-body non-equilibrium theory (e.g. entanglement growth, thermalization and localization, super- and subradiance, synchronization, driven-dissipative dynamics, time-dependent preparation of strongly-correlated phases of matter, ...) and to analyze their prospect for future applications in analog and digital quantum simulation & computation.